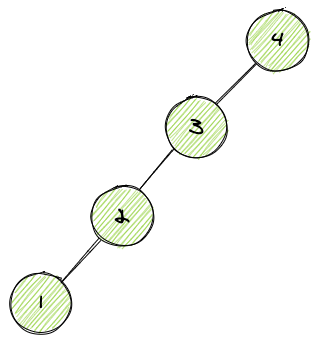
二叉树
二叉树是最简单的一种树形结构,每个节点最多有两个分支
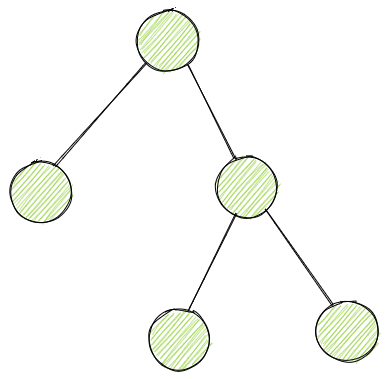
二叉搜索树(Binary Search Tree)
二叉搜索树,又叫二叉排序树,是一种有序的二叉树,每个节点的左边所有节点的值都比它小,右边所有的值都比它大
二叉搜索树即有链表快速插入与删除的特点,又有快速查找的优势
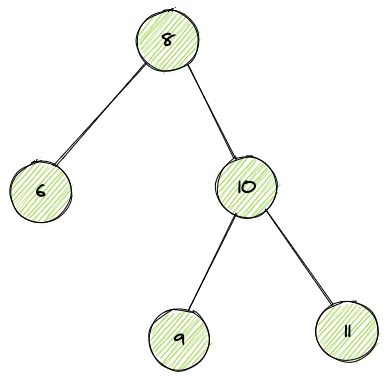
二叉搜索树查找某个元素所需要的最大次数等于树的层高。
假设节点数为n,层高为h,每个节点最多衍生2个子节点。因此
$$
\begin{align}
n &= 2^0 + 2^1 + 2^2 + … 2^{h-1} \\
2n &= 2^1 + 2^2 + … 2^{h} \\
两式相减得: n &= 2^h - 1 \\
h &= \log_2 (n+1)
\end{align}
$$
所以时间复杂度约为$O(\log_2 n)$
但极端情况下,二叉搜索树所有节点都集中在一边,二叉树退化为线性结构,此时层高h等于节点数n,时间复杂度为O(n)